 Lambda Diagrams
Lambda Diagrams
Lambda Diagrams are a graphical notation for closed lambda terms,
in which abstractions (lambdas) are represented by horizontal lines,
variables by vertical lines emanating down from their binding lambda,
and applications by horizontal links connecting the leftmost variables.
In the alternative style, applications link the nearest deepest variables,
for a more stylistic, if less uniform, look.
The following table shows diagrams of identity, the booleans, some standard combinators,
some Church numerals, the predecessor function on Church numerals, and Omega.
| term | definition | diagram | alternative |
| I/1 | λx.x |
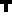 | |
| K/true | λx.λy.x |
 | |
| false/0 | λx.λy.y |
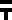 | |
| S | λx.λy.λz.(x z)(y z) |
 |
 |
| Y | λf.(λx.x x)(λx.f(x x)) |
 |
 |
| 2 | λf.λx.f(f x) |
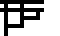 |
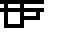 |
| 3 | λf.λx.f(f(f x)) |
 |
 |
| 4 | λf.λx.f(f(f(f x))) |
 |
 |
| pred | λn.λf.λx.n(λg.λh.h(g f))(λu.x)(λu.u) |
 |
 |
| fac | λn.λf.n(λf.λn.n(f(λf.λx.n f(f x))))(λx.f)(λx.x) |
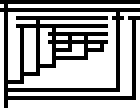 |
 |
| fib | λn.λf.n(λc.λa.λb.c b(λx.a (b x)))(λx.λy.x)(λx.x)f |
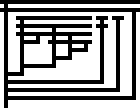 |
 |
| Ω | (λx.x x)(λx.x x) |
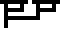 |
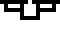 |
Curiously, the alternative Omega diagram somewhat resembles an (upside-down) Omega.
And here, on a larger scale, is a prime number sieve (alternative style):

which reduces to an infinite list of booleans that starts out as

Dimensions and complexity
In terms of pixels, a diagram's width is one less than 4 times the number of variables
(vertical lines),
and its height is one more than twice the maximum number of nested abstractions and applications
(one less for alternaitve diagrams with multiple variables).
The size of the binary encoding of a term is closely related to
the graphical complexity: it is exactly twice the number of lines
plus the number of (4-way) intersections.
Reduction
Beta-reduction on lambda diagrams can be shown in several steps, as demonstrated in this reduction
from Y=λf.(λx.x x)(λx.f(x x)) to λf.(λx.f(x x))(λx.f(x x))
| initial term |  |
| show application of abstraction | 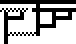 |
| show bound variables and argument | 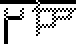 |
| expand function body |  |
| to make room for substitution | 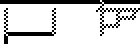 |
| substitute argument for variables |  |
| final term |  |
In the third frame, we show only the part of bound variables below abstractions, e.g. when
applying 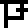 , the function body x(λy.x) shows as
, the function body x(λy.x) shows as 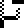 .
.
Diagrams In Motion
Paul Brauner has produced some awesome videos of beta reductions, produced with this software.
Youtuber 2swap made a cool video What is PLUS times PLUS? featuring animated lambda diagrams.
University of Oregon Ph.D. student Cruz Godar made a web app for animating colored lambda diagram's of one's choice.
Generalizing to non-closed terms
How could we denote unbound variables in a lambda diagram? We can imagine their
binding lambda to be somewhere invisibly above the diagram, so their vertical
line could stick out on top, not ending in any (visible) horizontal line.
Still, it's not clear how far different free variables should stick out. Except
if we assume the term is already in de-Bruijn notation. Then its index tells us
how many lambda binders need to be added in front of the term to bound the
variable. So we can let it stick out the appropriate amount. For a non-closed
term t, let n be the minimal so that λnt is closed. Then the diagram
for t could simply be the diagram for λnt with the n top lambdas not
drawn.
Related work
Dave Keenan has a comprehensive online paper
To Dissect a Mockingbird:
A Graphical Notation for the Lambda Calculus with Animated Reduction,
which partly inspired this page.
Alligator Eggs" is masquarading lambda calculus as a colorful puzzle game.
In his Master thesis, Viktor Massalõgin discusses 4 existing graphical notations before introducing his own "bubble" notation. Figure 3 on page 10 shows 4 depictions of the fixpoint combinator (which differs from Y above in one beta reduction), while the bubble form is in Figure 5 on page 13.
Prathyush Pramod compiled a catalogue of all known graphical notations.
λ-2D is a canvas based graphical notation allowing users to edit and run/animate code in a 2D grid..
Note
The diagram in the title, produced by the postscript code below, is a slightly deformed alternative Y diagram made to look like a Y.
%!PS-Adobe-2.0 EPSF-2.0
%%BoundingBox:0 0 118 110
/m{moveto}def/l{lineto}def/c{concat 6 m 0 6 l 7 8 m 0 8 l l l 3 6 l 2 6 m 7 6 l
3 4 m 6 4 l 6 6 l stroke}def 3 0 0 0 1[-8 4 0 8 60 9]c 3 2 0 2 2[-1 1 0 1 0 0]c
Back to my Binary Lambda Calculus page.
 Lambda Diagrams
Lambda Diagrams Lambda Diagrams
Lambda Diagrams





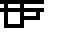










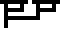
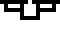



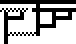
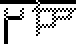

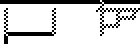


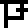 , the function body x(λy.x) shows as
, the function body x(λy.x) shows as 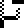 .
.