Which of these bitstrings are random?

01101000100000001000000000000000100000000000000000000000000000001000000000000000000000000000000000000000000000000000000000000000100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

01101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101100110100110010110100101100110100101101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001011010011001011010010110011010011001011001101001011010011001011001101001100101101001011001101001100101100110100101101001100101101001011001101001011010011001011001101001100101101001011001101001

01101110010111011110001001101010111100110111101111100001000110010100111010010101101101011111000110011101011011111001110111110111111000001000011000101000111001001001011001101001111010001010011010101010111011001011011011101011111100001100011100101100111101001101011101101101111110001110011110101110111111001111011111101111111000000100000110000101000011100010010001011000110100011110010001001001100101010010111001100100110110011101001111101000010100011010010101001110101001010101101011010101111011000101100110110101

11001001000011111101101010100010001000010110100011000010001101001100010011000110011000101000101110000000110111000001110011010001001010010000001001001110000010001000101001100111110011000111010000000010000010111011111010100110001110110001001110011011001000100101000101001010000010000111100110001110001101000000010011011101111011111001010100011001101100111100110100111010010000110001101100110000001010110000101001101101111100100101111100010100001101110100111111100001001101010110110101101101010100011100001001000101

The 512 bit lengths avoid mistakes made by articles such as this that claim

To illustrate, a sequence such as 00000000000000000000000000000000000000000000000000000000000000000000000000000000 can be described by a computer program much shorter than itself, namely: print 80 zeros

Just how much shorter? 14 bytes = 112 bits (or 98 bits of 7-bit ASCII).

We must avoid such bit vs byte confusion. Not engrave them in gold...

Algorithmic Information Theory

Ray J. Solomonoff (25 Jul 1926 – 7 Dec 2009)

November 1960 "A preliminary report on a general theory of inductive inference"

Technical Report ZTB-138, Zator Company, Cambridge, Massachusetts

Andrey N. Kolmogorov (25 Apr 1903 – 20 Oct 1987)

1965 "Three approaches to the definition of the quantity of information"

Problems of Information Transmission (1): 3–11.

Gregory J. Chaitin (25 Jun 1947 - )

1966 "On the Length of Programs for Computing Finite Binary Sequences"

Journal of the Association for Computing Machinery. 13 (4): 547–569.

Define the complexity of an object x relative to description method M as

K_M(x) = min {|p|: M(p) = x}

Objects can be binary strings, or natural numbers in a 1-1 correspondence:

 0  1  2  3  4  5  6   7   8   9  10  11 ...
 |  |  |  |  |  |  |   |   |   |   |   |
""  0  1 00 01 10 11 000 001 010 011 100 ...

(bitstring n is n+1 written in binary without its leading 1)

So we can take the length of a number, and consider that length as a binary string.

How do we avoid the description method parameter?

Call a description method U universal if for any other method M, we have that U complexities are at most a constant longer:

K_U(x) ≤ K_M(x) + O(1)

Invariance Theorem There is a universal description method U. Define K(x) = K_U(x)

Theorem K(x) is uncomputable

Theorem For strings of length n, K(x) ≤ n + O(1)

Theorem Fraction of { |x|= n, K(x) < n - c } is less than 2^-c

Chaitin's Incompleteness Theorem It's impossible to prove in general that a program p is elegant, i.e. of minimal length.

Some questions

What to make of K(<x,y>) ≤ K(x) + K(y) + ???

How to define a random infinite string x in terms of complexity of its prefixes x_1..n?

How to define an algorithmic probability P(x) ?

Prefix Complexity

Restrict programs to a prefix-free set, i.e. when p and q are different programs, then neither is a prefix of the other.

Define a universal prefix machine UP and corresponding complexity KP(x).

Call x random if KP(x) ≥ |x|.

Chaitin has a rather strong view on plain complexity:

"Anyway, in my opinion AIT really begins with my 1975 ACM Journal paper ``A theory of program size formally identical to information theory;'' the rest was the pre-history of the field!" Think of a computer as decoding equipment at the receiving end of a noiseless binary communications channel. Think of its programs as code words, and of the result of the computation as the decoded message. Then it is natural to require that the programs/code words form what is called a “prefix-free set,” so that successive messages sent across the channel (e.g. subroutines) can be separated.

Some Answers

KP(<x,y>) = KP(y) + KP(x|y*) + O(1)

KP(x) = KP(n) + KP(x|n*) + O(1), with n = |x|

An infinite binary string x is random if all but finitely many of its prefixes x_1..n are.

With probability 1, a randomly chosen infinite binary string is random.

This definition is equivalent to one by Per Martin-Löf from 1966 in terms of so-called constructive null-sets.

Algorithmic Probability

Define P(x) as the probability that the universal prefix machine outputs x.

Then P(x) = Θ(2^-KP(x))

So algorithmic probability is concentrated on the shortest program.

What is Ω = ∑_x P(x) ?

The number of wisdom (Chaitin)

Ω is the halting probability of UP on a random input. Ω is enumerable / semi-computable.

Theorem Ω is random

Many mathematical questions can (in theory) be settled by knowledge of the first few thousand bits of Ω.

Sketch: Ω_1..n, dovetail all programs contributing to Ω until their sum contribution exceeds Ω_1..n. At that point all unfinished programs up to length n are known not to halt.

Chaitin showed that proving the value of any k bits of Ω requires a formal theory of complexity at least k+O(1).

Making AIT concrete

Goals for universal machine

make programs as small as possible (no bit left behind)
as simple as possible
unify plain and prefix universal machines, and ones taking conditional arguments
allow rich variety of output: tuples, lists (finite and infinite), functions, ...

Chaitin's choice

In An Invitation to Algorithmic Information Theory,

DMTCS’96 Proceedings, Springer Verlag, Singapore, 1997, pp. 1–23,

Gregory Chaitin paraphrases John McCarthy about his invention of LISP, as "This is a better universal Turing machine. Let’s do recursive function theory that way!" Chaitin continues:

And the funny thing is that nobody except me has really I think taken that seriously. And the reason of course is that theoreticians didn't really much care about programming, about really playing with the computer. So the thing I've added is I think nowadays you have no excuse! If a theory has to do with the size of computer programs, you want to damn well see the programs, you want to be able to run them, it ought to be a programming language that is easy to use.

So I’ve done that using LISP because LISP is simple enough, LISP is in the intersection between theoretical and practical programming. Lambda calculus is even simpler and more elegant than LISP, but it’s unusable. Pure lambda calculus with combinators S and K, 11 it’s beautifully elegant, but you can’t really run programs that way, they’re too slow.

Turns out, neither is too slow to run programs. And while SK combinators are slightly simpler than lambda calculus, the latter is significantly more expressive, bit-for-bit. So that's what we're going with.

Let's build a pure functional machine

Functional bits

0 = λx₀ λx₁. x₀
1 = λx₀ λx₁. x₁

Input and output are lists built from cons as in LISP.

Unlike LISP, neither cons nor car/cdr/nil/null are primitives

cons = λx λy. (λz. z x y)
car = λL. L 0
car (cons T₀ T₁) = cons T₀ T₁ 0 = 0 T₀ T₁ = T₀
cdr = λL. L 1
cdr (cons T₀ T₁) = cons T₀ T₁1 = 1 T₀ T₁ = T₁

Functional binary strings/streams

nil = 1
null = λL. L (λh λt λx. false) true
null nil = nil (λh λt λx. false) true = 1 (λh λt λx. false) true = true
null (cons M N) = cons M N (λh λt λx. false) true = (λh λt λx. false) M N true = false
true = 0
false = 1

The booleans allow writing if bool then foo else bar as

 bool foo bar

car/cdr/null are mostly redundant

Instead of

if not null L then foo (car L) (cdr L) else bar

we can write

L (λh λt λ_. foo h t) bar

Or if L is known to be non-empty, simply

L foo

Lambda Machines

For a finite binary string s=b₀b₁..b_n-1 and lambda term T, denote by s:T the T-terminated list of its bits

cons b₀ (cons b₁ (cons ... (cons b_n-1 T)...)

A Lambda machine is a lambda calculus term M applied to a binary input stream that may or may not be terminated. The normalized result of this application is the output of the machine.

Example with identity machine ID = λx. x and input string 10

(λx. x) (cons 1 (cons 0 nil)) ->^* cons 1 (cons 0 nil)

showing ID (10:T) = (10:T). What does this say about K_ID(10) ?

A Universal Machine

We have shown how to translate bitstrings into lambda terms.

We'd now like to do the inverse: translate a lambda term M into a bitstring code(M). Then a Universal machine can operate as

U(code(M) : T} = M(T)

We thus need to encode

abstraction
application
variables

How to translate the latter?

Enter Dutch mathematician

Nicolaas de Bruijn

De Bruijn indices

De Bruijn came up with a name-free notation for variables in which each variable is replaced by the number of nested lambdas up to its binding lambda. For example, the pairing function

λx λy λz. z x y

is written

λ  λ  λ . 1 3 2

in De Bruijn notation (also known for his De Bruijn sequences).

Encoding lambda terms

First write a term in De Bruijn notation with application as prefix operator. The last example becomes

λ λ λ @ @ 1 3 2

Now encode

    λ as 00
    @ as 01
    n as 1ⁿ0

For example, code(λxλyλz. z x y) =

 code(λ λ λ @ @ 1 3 2) = 00 00 00 01 01 10 1110 110

A decoder

In my paper Functional Bits: Lambda Calculus based Algorithmic Information Theory, I derive a self-interpreter

E = (λ 1 1) (λ λ λ 1 (λ λ λ λ 3 (λ 5 (3 (λ 2 (3 (λ λ 3 (λ 1 2 3))) (4 (λ 4 (λ 3 1 (2 1)))))) (1 (2 (λ 1 2)) (λ 4 (λ 4 (λ 2 (1 4))) 5)))) (3 3) 2)

satisfying, for all closed terms M:

E C (code(M) : N) = C (λz. M) N

code(E) is 206 bits long !

For non-closed terms M, the result depends on what's passed in as z. We can pass in a term loop = (λx. x x)(λx. x x) to make the interpreter diverge in that case.

The Universal machine at last

U = E (λz.z loop)

satisfies

U(code(M) : T) = M(T)

code(U) =
    01010001101000000001010110000
    00000011110000101111110011110
    00010111001111000000111100001
    01101101110011111000011111000
    01011110100111010010110011100
    00110110000101111100001111100
    00111001101111011111001111011
    10110000110010001101000011010

Code optimality

token   λ    @    1   2    3     4      5      6+
freq   22   35   14   7    8     5      2      0
code   00   01   10 110 1110 11110 111110 111111*

U features the above code frequencies. The code lengths closely approximate an optimal Huffman code. A high indexed variable used several times within a local scope

λv. λ λ λ λ λ λ λ  (    ... v  ... v  ...)

can instead be re-bound with a single occurence to reduce code length:

λv. λ λ λ λ λ λ λ ((λv' ... v' ... v' ...) v)

AIT Made Concrete

We can finally define plain and prefix (conditional) complexities of lambda terms as

 K(x|y₁, . . . , y_k) = min{|p| | U (p : nil) y₁ . . . y_k = x}
KP(x|y₁, . . . , y_k) = min{|p| | U (p : T) y₁ . . . y_k = cons x T}

Through our standard encodings, we also obtain complexities of binary strings, pairs, tuple, lists, etc. E.g. for binary string s, K(s) = K(s : nil).

Note that programs consist of two parts: an encoded lambda term, and the bits that it "reads".

Programs terminated by nil are delimited while those with an unread tail T are self-delimiting. The latter by necessity form a prefix-free set.

Binary Lambda Calculus

Congratulations on making it this far!

BLC is the language of programs for the universal machine U. The simplest BLC programs are those starting with code(λx.x) = 0010 that prove

Theorem For strings x of length n, K(x) ≤ n + 4

What would be a good upperbound for KP(x) for strings x of length n?

Recall that KP(x) = KP(n) + KP(x|n*) + O(1) ≤ KP(n) + n + O(1)

Relating strings to numbers

We have the correspondence

 0  1  2  3  4  5  6   7   8   9  10  11 ...
 |  |  |  |  |  |  |   |   |   |   |   |
""  0  1 00 01 10 11 000 001 010 011 100 ...

Another way to relate them is in a tree...

Natural Binary Tree

natural numbers as vertices
binary strings as edges
2ⁿ length-n strings below vertex n
edge x goes from node |x| to x+1 (1w in binary)

Levenshtein coding

Vladimir Levenshtein discovered a prefix-free encoding that corresponds to concatenating the edges on the path from 0 to n, prefixed with a unary encoding of the depth of vertex n in the tree. Its definition is as simple as code(0) = 0, code(n+1) = 1 code(|n|) n

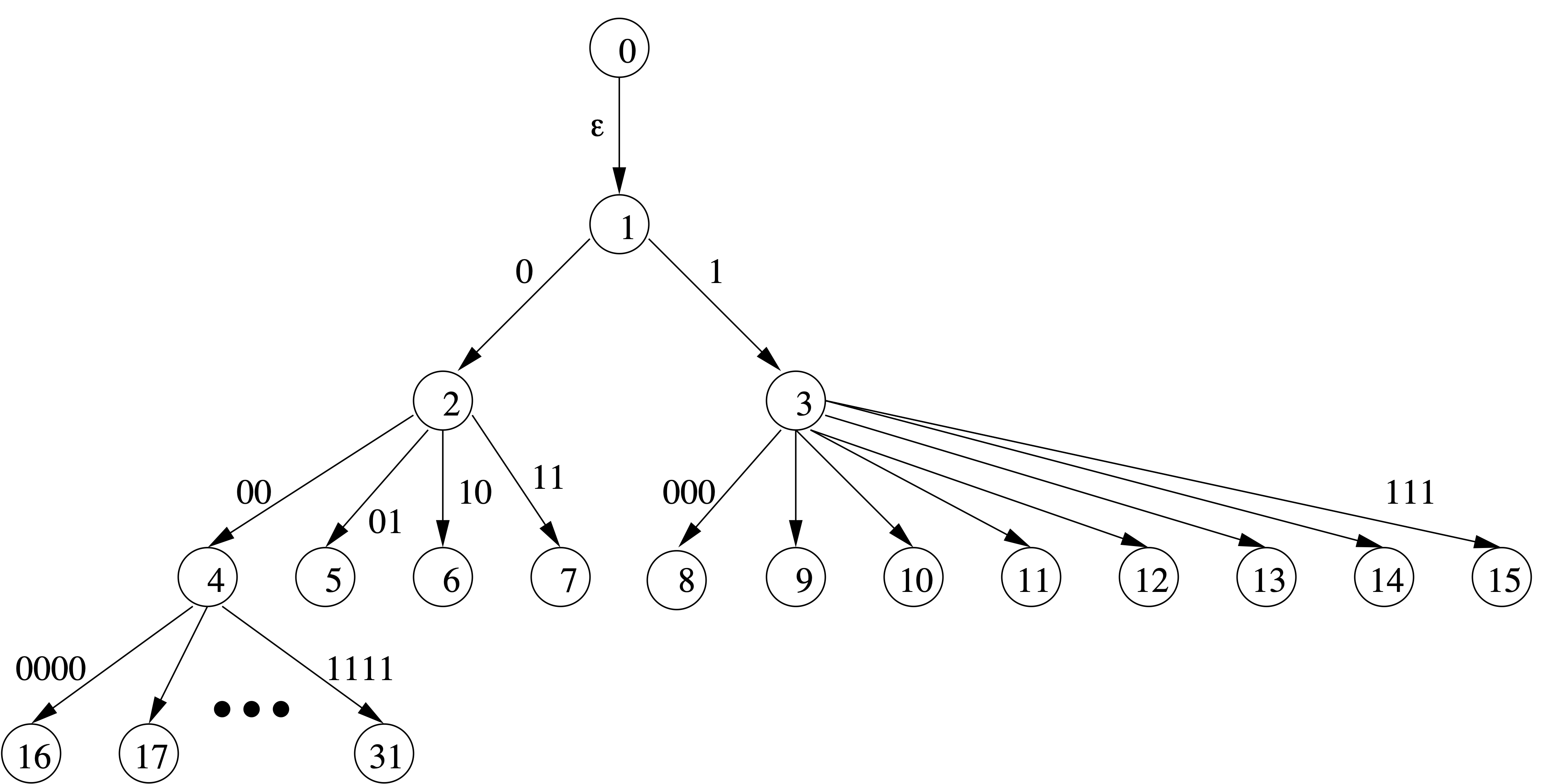
Number	String 	  Delimited
0		  0
1	0	  10
2	1	  110 0
3	00	  110 1
4	01	  1110 0 00
5	10	  1110 0 01
6	11	  1110 0 10
7	000	  1110 0 11
8	001	  1110 1 000
9	010	  1110 1 001
127     0000000   11110 0 10 111111

Levenshtein code properties

prefix-free and complete: ∑_n≥0 2^−|code(n)| = 1.
preserves numeric order as lexicographic one
simple to encode/decode
only O(log^*(n)) longer than optimal code for random x

Theorem For strings x of length n, KP(x) ≤ |code(x)| + 338

where 340 is the size of Levenshtein decoder

(λ 1 1) (λ λ λ 1 (λ 1 (3 (λ λ 1)) (4 4 (λ 1 (λ λ λ 1 (λ 4 (λ λ 5 2 (5 2 (3 1 (2 1)))))) 4 (λ 1))))) (λ λ λ 1 (3 ((λ 1 1) (λ λ λ λ 1 (λ 5 5 (λ λ 3 5 6 (λ 1 (λ λ 6 1 2) 3)) (λ λ 5 (λ 1 4 3))) (3 1)) (λ λ 1 (λ λ 2) 2) (λ 1)) (λ λ 1)) 2)

Most of that code is for converting from Church numeral back to bitstring. Leaving that part out, we get:

We can do even better for Church numerals: KP(Church_n) ≤ |code(n)| + 139 Theorem KP(Church numeral n) ≤ |code(n)| + 139

Complexity of Sets

A set of natural numbers can be identified with its characteristic sequence of bits, where bit i is 1 iff i is in the set.

Theorem KP(PRIMES) ≤ 167

where (prime number) 167 is the size of the prime number sieve

(λ 1 1) (λ λ λ 1 (λ 1 (3 (λ λ 1)) (4 4 (λ 1 (λ λ λ 1 (λ 4 (λ λ 5 2 (5 2 (3 1 (2 1)))))) 4 (λ 1))))) (λ λ λ 1 (3 ((λ 1 1) (λ λ 1 (λ λ λ 3 (λ 1 (λ λ 1) 3) (λ 1 (λ λ 2) (6 6 3))) (λ 1 (λ λ 2) 2))) (λ λ 1) ((λ 1 1) (λ λ λ λ 2 (4 4) (λ 1 4 2))) (λ λ 1)) 2)

Clearly, BLC is more of a compile target than a source code language.

The only nontrivial programs I hand-coded in BLC are the self interpreter and an SK interpreter.

A simple lambda calculus language

\io.let
   B0 = \x0\x1. x0;        -- bit 0
   B1 = \x0\x1. x1;        -- bit 1
   cons  = \x\y\z.z  x y;
   cons0 =   \y\z.z B0 y;
   Y = \f. (\x. x x) (\x. f (x x));

   -- Sieving numerals Sn = Ssucc^n S0

   S0    = \cont\x\xs. cons0  (xs cont);
   Ssucc = \Sn\c\x\xs. cons x (xs (Sn c));

   -- (x:xs) (Ssucc Sn cont) = Ssucc Sn cont x xs = x : xs (Sn cont)
   -- (list (Y Sn)) sets every (n+1)'th element of list to B0
   -- (11111111111111111111:T) (Y S0) = (00000000000000000000:T')
   -- (11111111111111111111:T) (Y S1) = (10101010101010101010:T')
   -- (11111111111111111111:T) (Y S2) = (11011011011011011011:T')

   sieve = \Sn. cons B1 (let Ssn = Ssucc Sn in (sieve Ssn) (Y Sn))
in cons0 (cons0 (sieve S0))

A BLC toolkit written in Haskell

$ ./blc help
Usage: blc action progfile [args]...
run	run given program applied to standard input bits and args
run8	run given program applied to standard input bytes and args
print	show program
nf	show normal form
hnf	show head normal form
nf_size	show size of normal form
comb_nf	normal form through SK reduction
comb	show translation to combinatory logic
bcw	encode in BCW combinators
bcl	encode in binary combinatory logic
diagram	show ascii diagram
Diagram	show alternative ascii diagram
boxchar	show boxdrawing character diagram
Boxchar	show boxdrawing character alternative diagram
pbm	show diagram in portable bitmap format
Pbm	show alternative diagram in portable bitmap format
tex	show program as TeX
html	show program as html
printlc	show lambda calculus program with de Bruijn indices
blc	encode as binary lambda calculus bits
Blc	encode as Binary lambda calculus bytes
size	show size in bits
help	show this text

Compiling to BLC

$ ../blc blc primes.lam 
00010001100110010100011010000000010110000010010001010111110111101001000110100001110011010000000000101101110011100111111101111000000001111100110111000000101100000110110$

Checking code size

$ ../blc size primes.lam 
167

Running the prime sieve

$ ../blc run primes.lam | head -c 64
0011010100010100010100010000010100000100010100010000010000010100$

Prime Art

$ ../blc Boxchar primes.lam 
─────────────────────────────────────────────────
┬─┬───────────────────────────────────┬──── ────┬
│ │ ┬─┬ ────┬─┬────────────────────── ┼───┬ ┬───┼
│ │ └─┤ ────┼─┼───────────────────┬── ┼───┼ │ ┬ │
│ │   │ ┬───┼─┼───────────────────┼── ┼─┬─┼ │ ┼ │
│ │   │ │ ─ ┼─┼─┬─────┬──── ──────┼─┬ │ ├─┘ └─┤ │
│ │   │ │ ┬ └─┤ │ ┬─┬ ┼─┬─┬ ──┬───┼─┼ ├─┘     ├─┘
│ │   │ └─┤   └─┤ └─┤ │ ├─┘ ──┼─┬─┼─┼ │       │  
│ │   │   │     │   │ ├─┘   ┬─┼─┼─┼─┼ │       │  
│ │   │   │     │   ├─┘     └─┤ │ ├─┘ │       │  
│ │   │   │     └───┤         │ ├─┘   │       │  
│ │   │   │         │         ├─┘     │       │  
│ │   │   │         ├─────────┘       │       │  
│ │   │   ├─────────┘                 │       │  
│ │   └───┤                           │       │  
│ │       ├───────────────────────────┘       │  
│ ├───────┘                                   │  
└─┤                                           │  
  └───────────────────────────────────────────┘

produces nice diagrams

Symmetry of Information I(x:y) = I(y:x)

Define information about x in y as I(x:y) = K(x) − K(x|y*)
Symmetry of Information says that y contains as much information about x as x does about y
Follows from K(x,y) = KP(x) + KP(y|x*) + O(1)

(λ 1 (λ λ 2) (λ 1 (λ λ 1)) (λ λ λ (λ 1 (3 2) (λ λ 3 1 (6 1 1 (4 ((λ 1 1) (λ λ λ λ λ 1 2 (λ 1 (λ λ 1) (λ λ λ 8 2) (λ λ 1) (4 (6 6) (λ 4 (λ 1 7 2)))))) 5) (λ λ 1) (λ λ λ λ 1) (λ λ 2) (λ λ 1)) (λ λ λ 1 (λ 1 6 4) 2))) (4 (λ 1) (λ 1) (λ 1) 1)) (λ 1)) (λ λ (λ 1 1) (λ λ λ λ 1 (λ (λ λ λ λ 3 (λ 6 (3 (λ 2 (3 (λ 14 (λ 3 (λ 1 2 3)))) (4 (λ 4 (λ 14 (3 1) (2 1)))))) (1 (2 (λ 1 2)) (λ λ 5 (λ 5 (λ 2 (1 5))) 7 6)) (λ 6 (λ 1 3 2)))) (λ 4 (λ 1 3 2))) (4 4) 3))

proves KP(x,y) ≤ KP(x)+KP(y|x*)+657, the easy side of the Theorem. Chaitin's version of the theorem has a constant of 2872, as the size of his LISP program

((’ (lambda (loop) ((’ (lambda (x*) ((’ (lambda (x) ((’ (lambda (y) (cons x (cons y nil)))) (eval (cons (’ (read-exp)) (cons (cons ’ (cons x* nil)) nil)))))) (car (cdr (try no-time-limit (’ (eval (read-exp))) x*)))))) (loop nil)))) (’ (lambda (p) (if(= success (car (try no-time-limit (’ (eval (read-exp))) p))) p (loop (append p (cons (read-bit) nil)))))))

using a resource bounded eval primitive "try".

Halting Probability

The lambda halting probability is defined as the probability that U will output any normal form:

Ω_λ = ∑ { 2^−|p| : U(p:T)=cons x T, x ∈ NF }

With some effort, we can determine the first 4 bits of this particular number of wisdom:

Ω_λ = .0001...

where probability .0001 = 2⁻⁴ is already contributed by programs 00100 and 00101 for terms True and False.

Beware Fake Omegas

If you see papers proclaiming to have computed many dozens of Omega bits, then their universal machine is very wasteful with bits. Or not even universal, such as in this paper, where each data bit is counted as contributing 7 or 8 bits to the program length!

Busy Beaver

Entry A333479 of the amazing Online Encyclopedia of Integer Sequences defines a BLC inspired Busy Beaver function as the maximum normal form size of any closed lambda term of size n. This is like an inverse of K_min(x) = min { K(y) : y ≥ x }, particularly if those shortest programs consist of only the encoded lambda term. Curiously, the 63 bit Busy Beaver already far exceeds Graham's number, as witnessed by lambda term (λ 1 (1 (λ λ λ 1 3 2 1) 1) 1 1) (λ λ 2 (2 1)), giving a whole new meaning to the question of what's the largest number representable in 64 bits...

Byte sized IO

While bit streams are nice in theory, they fare poorly in interfacing with the real world. In the practice oriented BLC8, programs operate on a stream of bytes, each represented as a delimited list of 8 bits in big-endian order.

BLC8 requires a more complicated universal machine:

U8 = λ 1 ((λ 1 1) (λ (λ λ λ 1 (λ λ λ 2 (λ λ λ (λ 7 (10 (λ 5 (2 (λ λ 3 (λ 1 2 3))) (11 (λ 3 (λ 3 1 (2 1))))) 3) (4 (1 (λ 1 5) 3) (10 (λ 2 (λ 2 (1 6))) 6))) 8) (λ 1 (λ 8 7 (λ 1 6 2)))) (λ 1 (4 3))) (1 1)) (λ λ 2 ((λ 1 1) (λ 1 1))))

The parser in U8 keeps track of both remaining bytes, and remaining bits in the current byte, discarding the latter when parsing is completed.

The size of U8, which is 355 bits as a BLC program, is 45 bytes in BLC8.

International Obfuscated C Code Contest

In 2012, I submitted this BLC interpreter to the 21st IOCCC:

and won in the category of Most functional.

Dessert Time

First in Haskell

--         1   1   1 * 2   1 * 2 * 3   1 * 2 * 3 * 4
-- pi/2 =  - + - + ----- + --------- + ------------- + ...
--         1   3   3 * 5   3 * 5 * 7   3 * 5 * 7 * 9
-- sum first n terms < pi/2 < sum first n terms + n'th term
-- a/c is 2^j times the sum of the first n terms minus the value of the j bits already output
-- b/c is 2^j times the n-th term product [1..n] / product [1,3..2*n+1]
halfpi = go 1 1 1 1 where
  go b a c = 
    if a >= c
      then                \n. 1 : go (2*b) (2*(a-c) )  c       n
      else if a + b < c
        then              \n. 0 : go (2*b) (2* a    )  c       n
        else \n -> let
          n21 = 2*n + 1
          bn = b*n
        in                        go    bn (a*n21+bn) (c*n21) (n+1)

How to do addition, subtraction, multiplication, comparison in BLC concisely?

Use mix of Church and Tuple numerals

\io. let
  id = \x. x; bit0 = \x0\x1. x0; bit1 = \x0\x1. x1; cons = \a\b\p. p a b;
  C1 = id;
  Csucc = \n\f\x. f (n f x);
  Cadd = \a\b\f\x. a f (b f x);
  -- Tm x (Tn y) = if n < m then y (Tm-1-n x) else x (Tn-m y)
  T1 = \x\f. f x;
  Tadd = \tm\tn\x. tm (tn x);
  Tsub = \tm\tn\x. tm id (tn x);
  CTmul = \c\t. c t;
  go = \Tb\Ta\Tc. let
      prod = \bit\Ta'\Cn. cons bit (go (Tadd Tb Tb) (Tadd Ta' Ta') Tc Cn) in
      (Tc (\_. prod bit1 (Tsub Tc Ta)))      -- case Ta >= Tc
      (Ta (\_.                               -- case Ta < Tc
         (Tc
             (\_\Cn. let                     -- case Ta+Tb >= Tc
                    x2np1 = CTmul (Csucc (Cadd Cn Cn));
                    CnxTb = CTmul Cn Tb
              in go CnxTb (Tadd (x2np1 Ta) CnxTb) (x2np1 Tc) (Csucc Cn)))
         (Ta (Tb (\_. prod bit0 Ta)))        -- case Ta+Tb < Tc
      ));
in go T1 T1 T1 C1;

Binary Lambda Calculus:

The Smallest Program Language

Overview